Lösung der Aufgabe für unterwegs
Die Frage war: Wieviele Quadrate gibt es auf einem Schachbrett?
Als allererstes werdet ihr sicher sagen: "klar das Schachbrett hat 64 Felder, also sind auf dem Schachbrett 64 Quadrate". Aber wenn ihr nochmals genau hinschaut, bemerkt ihr sicher, dass das Brett selbst schon ein Quadrat ist. Auch gibt es viele Quadrate mit der Kantenlänge 2 wie ihr in dem folgenden Diagramm beispielhaft seht:
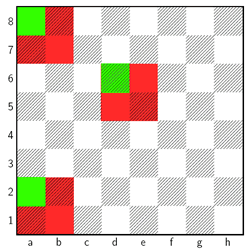
Natürlich gibt es auch Quadrate mit Kantenlänge 3, 4, 5, 6, usw. Ihr könnt euch sicher vorstellen, dass es ganz schön viele Quadrate werden!
Richtig geschätzt habt ihr, wenn ihr "c) mehr als 200 Quadrate" gesagt habt. Genau sind es 204 Quadrate. Aber das rauszufinden ist gar nicht leicht, obwohl es eigentlich nur zählen ist, was man machen muss -- es ist nämlich sehr viel zu zählen!
Wenn man geschickt zählt kommt man schneller drauf: Im letzten Diagramm habe ich das linke obere Feld eines Quadrats grün gemalt. Wenn ich alle Felder grün anmale, bei denen ich die linke obere Ecke eines 2x2-Quadrats hereinsetzen kann, sieht das so aus:
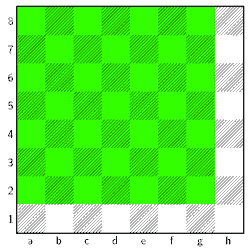
Am Rand passen keine 2x2 Quadrate mehr rein. Es gibt also 7x7 = 49 solche Quadrate. Genauso kann man sich überlegen, dass es 6x6 = 36 Quadrate mit Kantenlänge 3 gibt usw. Am Ende sieht man dann, dass es 1x1 + 2x2 + 3x3 + 4x4 + 5x5 + 6x6 + 7x7 + 8x8 = 204 Quadrate gibt. Wenn ihr das selber herausbekommen habt, was wie schon gesagt, nicht verlangt war, dann allen Respekt!
Weiter zur nächsten Station geht's hier.
