Daneben!

Ihr habt euch wohl verlaufen, richtig wäre folgendes gewesen:

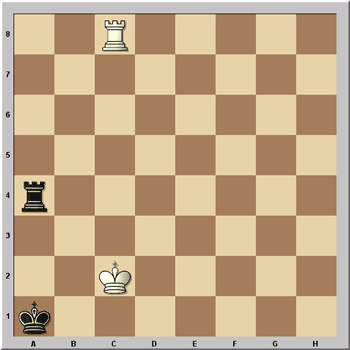
Die Frage war: Wie steht es hier (Weiß am Zug)?

Weiß steht hier tatsächlich auf Gewinn! Es stimmt zwar schon, dass das Endspiel Turm gegen Turm in der Regel Remis ist, aber hier liegt eben eine Ausnahme vor. Weiß hat nämlich den starken Zug 1. Kc2-b3 in der Hinterhand, womit er nicht nur den schwarzen Turm auf a4 angreift, sondern auch den Weg für den Turm auf c8 frei macht, der jetzt auf c1 matt zu setzen droht. Schwarz verliert nun seinen Turm und das entstehende Endspiel ist dann bekanntlich für Weiß gewonnen.

Die Frage war: Wieviele Stellungen können in einer Schachpartie entstehen, nachdem Weiß und Schwarz jeweils einen Zug gemacht haben?

Mal zählen: Weiß kann mit seinen acht Bauern ein oder zwei Felder ziehen -- macht 16 Zugmöglichkeiten; dazu kommen die vier Springerzüge nach a3, c3, f3 und h3. Weiß hat also in seinem ersten Zug 20 unterschiedliche Zugmöglichkeiten. Auf jeden dieser 20 Züge von Weiß kann auch Schwarz aus 20 möglichen wählen -- insgesamt haben wir also 20 mal 20 = 400 verschiedene Stellungen nach einem Zug!

Lauft jetzt zurück zum letzten Posten (hier auf dem Rechner ist das nicht sonderlich beschwerlich -- ein Klick auf den "Zurück-Button" bzw. das Drücken der backspace-Taste genügt). Da ihr nun die Lösungen kennt, findet ihr von dort den richtigen Weg, oder?!